GLM Basis Functions

[1]:

# This cells setups the environment when executed in Google Colab.
try:
    import google.colab
    !curl -s https://raw.githubusercontent.com/ibs-lab/cedalion/dev/scripts/colab_setup.py -o colab_setup.py
    # Select branch with --branch "branch name" (default is "dev")
    %run colab_setup.py
except ImportError:
    pass

[2]:

import cedalion
import cedalion.models.glm.basis_functions as bf
import cedalion.models.glm.design_matrix as dm

import cedalion.dataclasses as cdc

import matplotlib.pyplot as p
import numpy as np
import xarray as xr
import matplotlib.pyplot as p
import cedalion.datasets

units = cedalion.units

xr.set_options(display_expand_data=False)

[2]:

<xarray.core.options.set_options at 0x7f6f78f27010>

[3]:

# dummy time series
fs = 8.0
ts = cdc.build_timeseries(
    np.random.random((100, 1, 2)),
    dims=["time", "channel", "chromo"],
    time=np.arange(100) / fs,
    channel=["S1D1"],
    value_units=units.uM,
    time_units=units.s,
    other_coords={'chromo' : ["HbO", "HbR"]}
)
display(ts)

<xarray.DataArray (time: 100, channel: 1, chromo: 2)> Size: 2kB
[µM] 0.7185 0.8201 0.7566 0.7754 0.2139 ... 0.8349 0.1311 0.7664 0.749 0.9798
Coordinates:
  * time     (time) float64 800B 0.0 0.125 0.25 0.375 ... 12.0 12.12 12.25 12.38
    samples  (time) int64 800B 0 1 2 3 4 5 6 7 8 ... 91 92 93 94 95 96 97 98 99
  * channel  (channel) <U4 16B 'S1D1'
  * chromo   (chromo) <U3 24B 'HbO' 'HbR'
[4]:

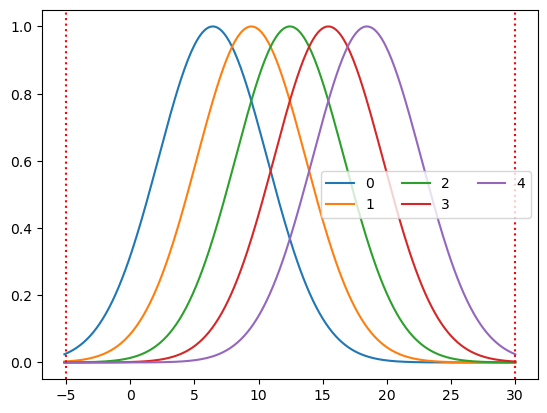
basis = bf.GaussianKernels(
    t_pre=5 * units.s,
    t_post=30 * units.s,
    t_delta=3 * units.s,
    t_std=3 * units.s,
)
hrf = basis(ts)

p.figure()
for i_comp, comp in enumerate(hrf.component.values):
    p.plot(hrf.time, hrf[:, i_comp], label=comp)

p.axvline(-5, c="r", ls=":")
p.axvline(30, c="r", ls=":")
p.legend(ncols=3)

[4]:

<matplotlib.legend.Legend at 0x7f6f5dfbbc50>
../../_images/examples_modeling_31_glm_basis_functions_4_1.png 
[5]:

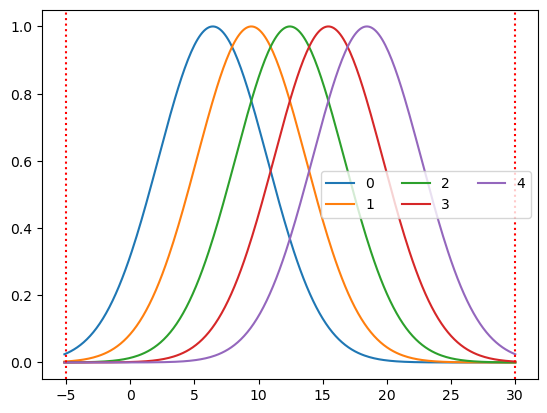
basis = bf.GaussianKernelsWithTails(
    t_pre=5 * units.s,
    t_post=30 * units.s,
    t_delta=3 * units.s,
    t_std=3 * units.s,
)
hrf = basis(ts)

p.figure()
for i_comp, comp in enumerate(hrf.component.values):
    p.plot(hrf.time, hrf[:, i_comp], label=comp)
p.axvline(-5, c="r", ls=":")
p.axvline(30, c="r", ls=":")
p.legend(ncols=3)

[5]:

<matplotlib.legend.Legend at 0x7f6f5dfde890>
../../_images/examples_modeling_31_glm_basis_functions_5_1.png 
[6]:

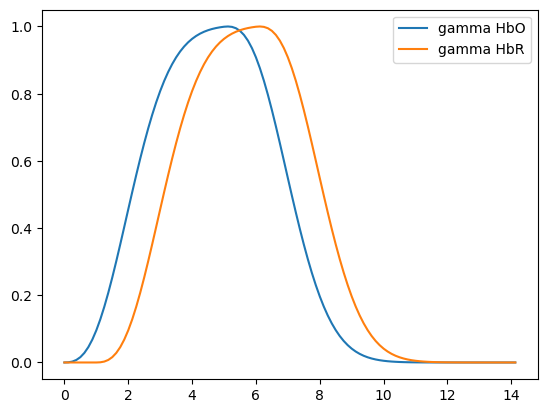
basis = bf.Gamma(
    tau={"HbO": 0 * units.s, "HbR": 1 * units.s},
    sigma=3 * units.s,
)
hrf = basis(ts)
display(hrf)
p.figure()
for i_comp, comp in enumerate(hrf.component.values):
    for i_chromo, chromo in enumerate(hrf.chromo.values):
        p.plot(hrf.time, hrf[:, i_comp, i_chromo], label=f"{comp} {chromo}")

p.legend()

<xarray.DataArray (time: 107, component: 1, chromo: 2)> Size: 2kB
0.0 0.0 0.004711 0.0 0.01875 ... 2.533e-07 3.574e-06 1.789e-07 2.601e-06
Coordinates:
  * time       (time) float64 856B 0.0 0.125 0.25 0.375 ... 13.0 13.12 13.25
  * chromo     (chromo) <U3 24B 'HbO' 'HbR'
  * component  (component) <U5 20B 'gamma'
[6]:

<matplotlib.legend.Legend at 0x7f6f5dddcf50>
../../_images/examples_modeling_31_glm_basis_functions_6_2.png 
[7]:

basis = bf.Gamma(
    tau={"HbO": 0 * units.s, "HbR": 1 * units.s},
    sigma=2 * units.s,
)
hrf = basis(ts)
display(hrf)

p.figure()
for i_comp, comp in enumerate(hrf.component.values):
    for i_chromo, chromo in enumerate(hrf.chromo.values):
        p.plot(hrf.time, hrf[:, i_comp, i_chromo], label=f"{comp} {chromo}")

p.legend()

<xarray.DataArray (time: 74, component: 1, chromo: 2)> Size: 1kB
0.0 0.0 0.01058 0.0 0.04181 ... 7.789e-06 8.836e-08 4.894e-06 5.155e-08 3.05e-06
Coordinates:
  * time       (time) float64 592B 0.0 0.125 0.25 0.375 ... 8.75 8.875 9.0 9.125
  * chromo     (chromo) <U3 24B 'HbO' 'HbR'
  * component  (component) <U5 20B 'gamma'
[7]:

<matplotlib.legend.Legend at 0x7f6f5cd77a10>
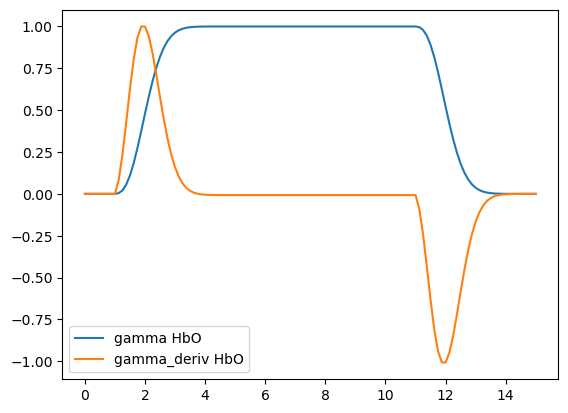
../../_images/examples_modeling_31_glm_basis_functions_7_2.png 
[8]:

basis = bf.GammaDeriv(
    tau=2 * units.s,
    sigma=2 * units.s,
)
hrf = basis(ts)
display(hrf)
p.figure()
for i_comp, comp in enumerate(hrf.component.values):
    for i_chromo, chromo in enumerate(["HbO"]):
        p.plot(hrf.time, hrf[:, i_comp, i_chromo], label=f"{comp} {chromo}")

p.legend()

<xarray.DataArray (time: 82, component: 2, chromo: 2)> Size: 3kB
0.0 0.0 0.0 0.0 0.0 0.0 ... -2.311e-05 3.05e-06 3.05e-06 -1.466e-05 -1.466e-05
Coordinates:
  * time       (time) float64 656B 0.0 0.125 0.25 0.375 ... 9.875 10.0 10.12
  * chromo     (chromo) <U3 24B 'HbO' 'HbR'
  * component  (component) <U11 88B 'gamma' 'gamma_deriv'
[8]:

<matplotlib.legend.Legend at 0x7f6f5cd63650>
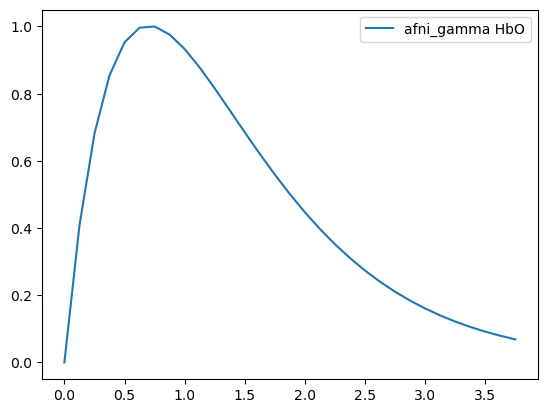
../../_images/examples_modeling_31_glm_basis_functions_8_2.png 
[9]:

basis = bf.AFNIGamma(
    p=1,
    q=0.7 * units.s,
)
hrf = basis(ts)
display(hrf)
p.figure()
for i_comp, comp in enumerate(hrf.component.values):
    for i_chromo, chromo in enumerate(["HbO"]):
        p.plot(hrf.time, hrf[:, i_comp, i_chromo], label=f"{comp} {chromo}")

p.legend()

<xarray.DataArray (time: 31, component: 1, chromo: 2)> Size: 496B
0.0 0.0 0.407 0.407 0.6809 0.6809 ... 0.0918 0.07953 0.07953 0.06882 0.06882
Coordinates:
  * time       (time) float64 248B 0.0 0.125 0.25 0.375 ... 3.375 3.5 3.625 3.75
  * chromo     (chromo) <U3 24B 'HbO' 'HbR'
  * component  (component) <U10 40B 'afni_gamma'
[9]:

<matplotlib.legend.Legend at 0x7f6f5cc2bcd0>
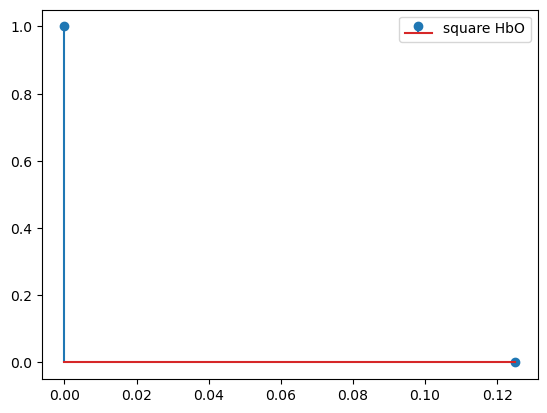
../../_images/examples_modeling_31_glm_basis_functions_9_2.png 
[10]:

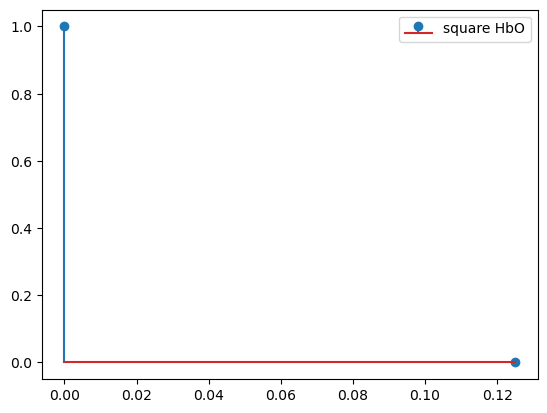
basis = bf.DiracDelta()
hrf = basis(ts)
display(hrf)
p.figure()
for i_comp, comp in enumerate(hrf.component.values):
    for i_chromo, chromo in enumerate(["HbO"]):
        p.stem(hrf.time, hrf[:, i_comp, i_chromo], label=f"{comp} {chromo}")

p.legend()

<xarray.DataArray (time: 2, component: 1, chromo: 2)> Size: 32B
1.0 1.0 0.0 0.0
Coordinates:
  * time       (time) float64 16B 0.0 0.125
  * chromo     (chromo) <U3 24B 'HbO' 'HbR'
  * component  (component) <U6 24B 'square'
[10]:

<matplotlib.legend.Legend at 0x7f6f5caefdd0>
../../_images/examples_modeling_31_glm_basis_functions_10_2.png